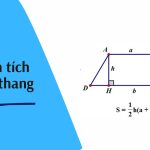
Công thức lượng giác đóng vai trò như một chiếc chìa khóa vạn năng giúp khai mở những bài toán hình học và đại số hóc búa nhất. Việc nắm vững các quy luật biến đổi hàm số góc không chỉ giúp cải thiện điểm số mà còn phát triển tư duy logic vượt trội. Bạn hoàn toàn có thể tìm thấy sự tự tin và phong cách học tập mới mẻ cùng sự đồng hành từ thương hiệu SevenAM.
Tầm quan trọng của các công thức lượng giác hiện nay
Trong hệ thống giáo dục hiện đại, việc tiếp cận các quy luật tính toán liên quan đến tam giác và vòng tròn đơn vị luôn là thử thách lớn với nhiều người. Những kiến thức này không đơn thuần là những con số khô khan mà còn là ngôn ngữ để mô tả các hiện tượng vật lý trong đời sống.
Nghiên cứu cho thấy những cá nhân thành thạo việc biến đổi các biểu thức toán học thường có khả năng phân tích dữ liệu tốt hơn trong môi trường làm việc thực tế. Hệ thống các ký hiệu và định lý này được xây dựng qua hàng thế kỷ, kết tinh từ trí tuệ của các nhà toán học lỗi lạc nhằm đơn giản hóa những phép đo phức tạp. Khi bạn nhìn thấu được sự liên kết giữa các góc và cạnh, mọi bài tập sẽ không còn là rào cản ngăn bước tiến của bạn trên con đường học vấn.

Hệ thống hóa các công thức lượng giác quan trọng nhất
Việc phân loại các nhóm biến đổi giúp người học dễ dàng tra cứu và áp dụng vào từng dạng bài tập cụ thể một cách linh hoạt. Phần nội dung dưới đây sẽ cung cấp cái nhìn chi tiết về các nhóm biến đổi từ cơ bản đến chuyên sâu trong công thức lượng giác để bạn đọc dễ dàng hệ thống lại kiến thức.
Nhóm biến đổi cộng cung
Các phép tính cộng hoặc trừ giữa các góc tạo ra những kết quả thú vị, cho phép chúng ta chia nhỏ các góc lớn thành những thành phần đơn giản hơn để xử lý. Đây là nền tảng then chốt để khai triển các biểu thức phức tạp hơn trong những kỳ thi quan trọng sắp tới của bạn.
Phép biến đổi nhân đôi
Khi một góc được tăng quy mô lên hai lần, giá trị hàm số của chúng sẽ tuân theo những quy tắc đặc thù để duy trì sự cân bằng của phương trình. Những biểu thức này thường xuyên xuất hiện trong các bài toán tích phân và đạo hàm, yêu cầu sự chính xác tuyệt đối trong từng bước chuyển đổi.
Ứng dụng công thức lượng giác biến đổi tích
Việc chuyển đổi từ một tích các hàm số sang dạng tổng hoặc hiệu là một kỹ thuật tinh tế giúp đơn giản hóa quá trình tính toán đáng kể. Kỹ năng này đòi hỏi sự nhạy bén trong việc nhận diện các mẫu số chung và sự tương quan giữa các đại số trong một hệ thống đóng.
Biến đổi tổng thành tích
Ngược lại với phép toán công thức lượng giác trên, việc đưa các biểu thức dạng tổng về dạng tích giúp chúng ta dễ dàng tìm ra nghiệm của các phương trình bậc cao hoặc phương trình lượng giác. Đây là công cụ đắc lực mà bất kỳ chuyên gia toán học nào cũng cần phải nằm lòng để tối ưu hóa thời gian làm bài.
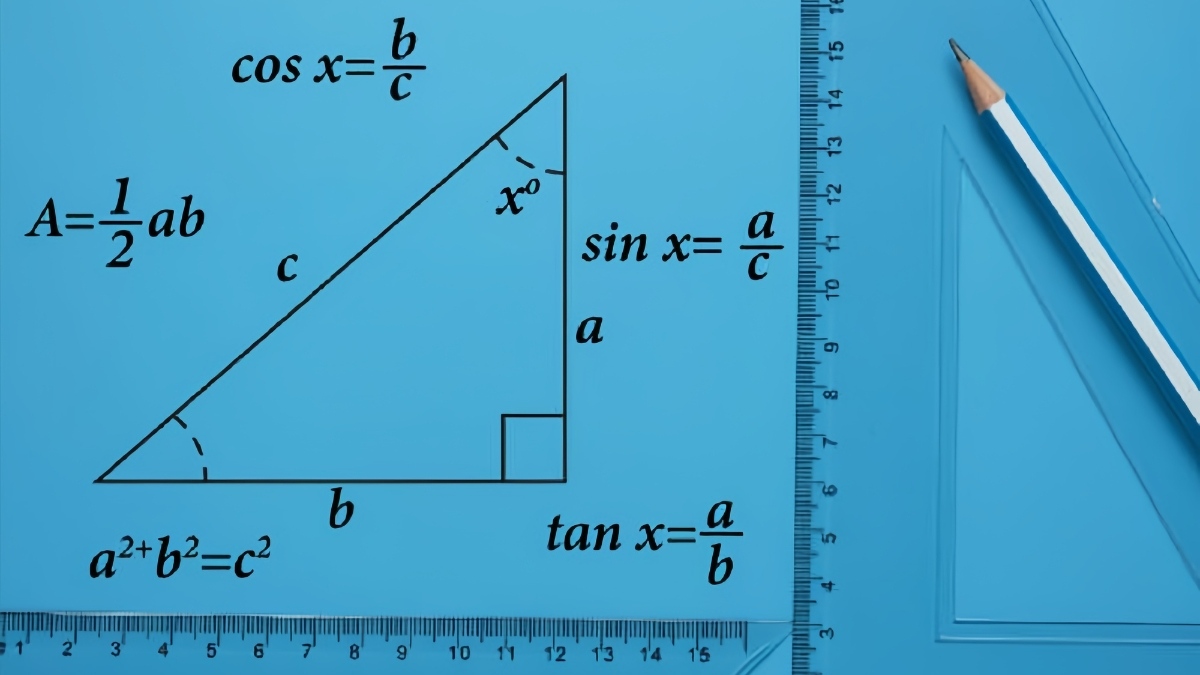
Phương pháp ghi nhớ công thức lượng giác nhanh chóng
Để không bị nhầm lẫn giữa một rừng các ký hiệu, việc áp dụng những mẹo ghi nhớ bằng thơ hoặc hình ảnh là một chiến thuật vô cùng thông minh. Dưới đây là những cách tiếp cận sáng tạo giúp các kiến thức lý thuyết về công thức lượng giác trở nên sinh động và dễ đi vào tiềm thức của bạn hơn bao giờ hết.
- Sử dụng những câu thơ lục bát có vần điệu để liên kết các giá trị sin và cos trong phép toán cộng hoặc trừ một cách tự nhiên.
- Xây dựng mối liên hệ giữa các hàm số với những hình ảnh thực tế giúp não bộ lưu trữ thông tin lâu hơn so với cách học vẹt thông thường.
- Thường xuyên thực hành việc tự thiết lập lại các công thức lượng giác từ những nguyên lý cơ bản để hiểu rõ nguồn gốc của chúng.
- Tạo ra các sơ đồ tư duy đa màu sắc nhằm phân tách các nhóm biến đổi theo từng chủ đề riêng biệt để dễ dàng đối chiếu khi cần thiết.
- Áp dụng các phần mềm giả lập đồ thị để quan sát sự thay đổi của hàm số khi các biến số góc được điều chỉnh trực tiếp trên màn hình.
- Tham gia các nhóm học tập để cùng trao đổi về những phương pháp giải toán mới lạ, từ đó củng cố thêm kiến thức đã tiếp thu.
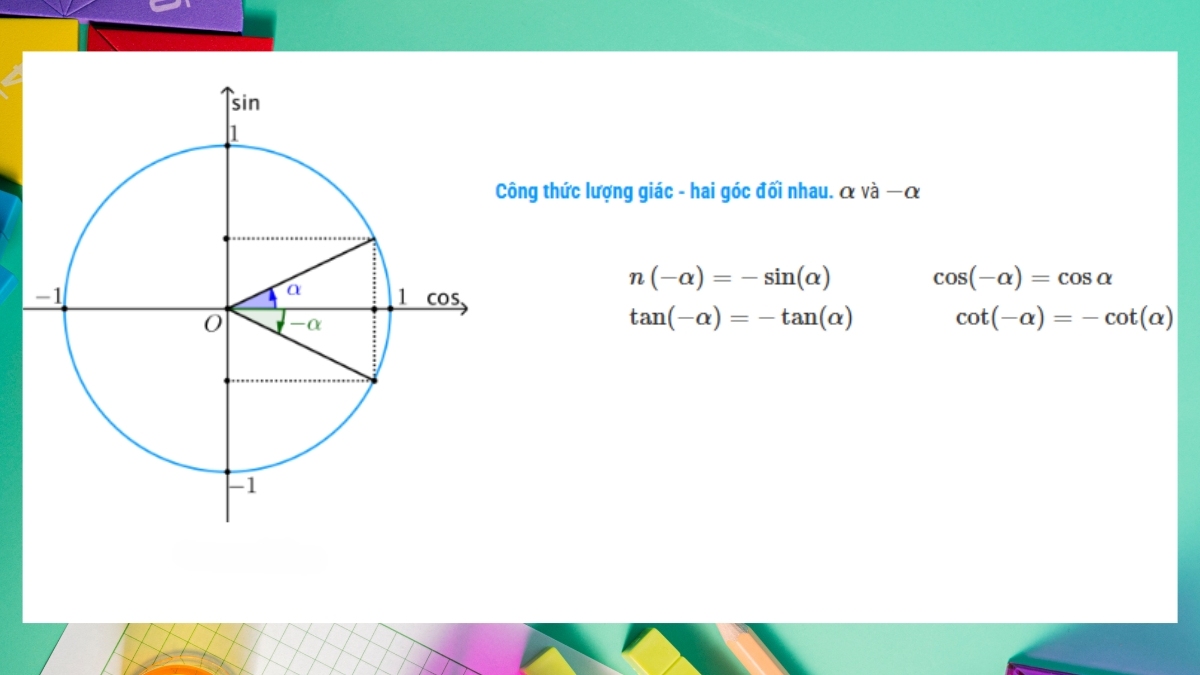
Ứng dụng thực tiễn của công thức lượng giác đời sống
Không chỉ nằm trên những trang giấy, các hệ thức này trong công thức lượng giác còn hiện diện trong kiến trúc, thiên văn học và cả công nghệ xử lý âm thanh kỹ thuật số.
Ngành kiến trúc xây dựng
Các kiến trúc sư sử dụng những tính toán này để xác định độ dốc của mái nhà hoặc lực chịu tải của các thanh đà trong những công trình cao tầng. Độ chính xác của các phép tính liên quan đến góc sẽ đảm bảo sự an toàn và bền vững cho toàn bộ cấu trúc công trình theo thời gian.
Công nghệ âm thanh ánh sáng
Sóng âm và ánh sáng vốn bản chất là những dao động tuần hoàn, do đó việc phân tích chúng không thể thiếu sự can thiệp của các hàm số tuần hoàn. Việc điều chỉnh tần số và biên độ để tạo ra âm thanh trong trẻo chính là sự ứng dụng thực tế sinh động nhất của toán học vào nghệ thuật.
Lĩnh vực hàng không vũ trụ
Trong việc định vị vệ tinh hoặc điều hướng đường bay cho phi cơ, các phép tính lượng giác cầu đóng vai trò quyết định đến sự thành bại của mỗi chuyến đi. Mọi sai sót nhỏ trong việc tính toán góc độ đều có thể dẫn đến những hậu quả nghiêm trọng, đòi hỏi sự kiểm soát gắt gao từ các hệ thống máy tính.
Kết luận
Công thức lượng giác thực sự là một phần quan trọng tạo nên vẻ đẹp logic và sự chặt chẽ của nền toán học toàn cầu. Việc am hiểu tường tận các quy luật này không chỉ giúp bạn chinh phục mọi kỳ thi mà còn mở ra tầm nhìn rộng lớn về cách thế giới vận hành. Hãy bắt đầu hành trình khám phá những con số ngay hôm nay để khẳng định bản thân và đừng quên ghé thăm SevenAM để cập nhật thêm nhiều thông tin hữu ích nhé.