Đạo hàm đóng vai trò là một trong những cột mốc quan trọng nhất trong hành trình chinh phục toán học giải tích của mọi học sinh lớp 11. Việc thấu hiểu bản chất của khái niệm này không chỉ giúp hoàn thành tốt các kỳ thi mà còn mở ra tư duy logic sắc bén để ứng dụng vào thực tế đời sống. Hãy cùng khám phá những kiến thức bổ ích này cùng thương hiệu thời trang SevenAM.
Tổng quan về khái niệm đạo hàm trong chương trình toán học
Xét về bản chất toán học sơ cấp, thực thể này đại diện cho tỷ lệ thay đổi tức thời của một hàm số tại một điểm cụ thể trên trục tọa độ phẳng. Khi biến số độc lập trải qua một sự điều chỉnh cực nhỏ, giá trị đầu ra tương ứng sẽ dao động theo một quy luật mà phép toán này có khả năng mô tả chính xác tuyệt đối. Các nhà khoa học lỗi lạc như Isaac Newton đã đặt nền móng cho khái niệm này nhằm giải thích các hiện tượng vật lý phức tạp liên quan đến chuyển động và lực tác động.
Việc tiếp cận phép toán này đòi hỏi người học phải có nền tảng vững chắc về giới hạn, bởi lẽ nó chính là kết quả của một quá trình tiệm cận khi khoảng cách giữa hai điểm trên đồ thị dần tiến về con số không tròn trĩnh. Nếu không có công cụ này, chúng ta sẽ gặp muôn vàn khó khăn trong việc xác định độ dốc của một đường cong tại một vị trí duy nhất, điều vốn dĩ không thể thực hiện bằng các phương pháp hình học phẳng thông thường.
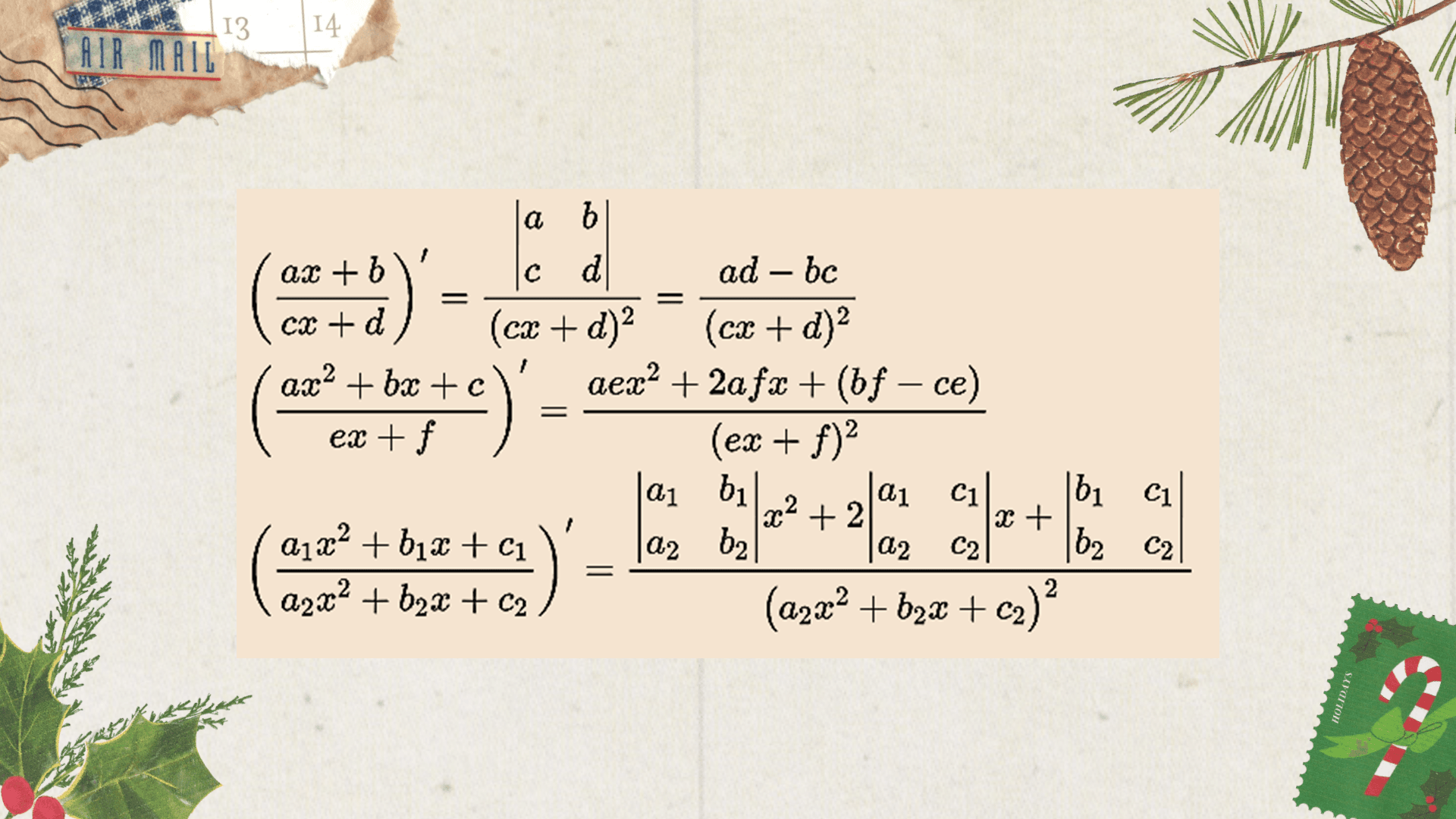
Các quy tắc tính toán đạo hàm cơ bản cần ghi nhớ kỹ
Để xử lý các biểu thức đại số phức tạp, bạn cần nắm vững những nguyên tắc nền tảng giúp đơn giản hóa quá trình biến đổi các ký hiệu toán học. Việc áp dụng linh hoạt các công thức này không chỉ tiết kiệm thời gian mà còn hạn chế tối đa những sai sót đáng tiếc trong quá trình làm bài thi.
Quy tắc cộng hiệu
Khi đối mặt với một đa thức bao gồm nhiều thành phần liên kết bởi dấu cộng hoặc trừ, bạn chỉ cần thực hiện phép toán cho từng hạng tử riêng biệt rồi kết hợp lại. Điều này giúp chia nhỏ bài toán lớn thành các phần việc đơn giản và dễ kiểm soát hơn.
Quy tắc nhân chia
Phép tính dành cho tích hoặc thương của hai hàm số đòi hỏi sự cẩn trọng cao hơn vì cấu trúc của kết quả không đơn thuần là tích hay thương của các thành phần riêng lẻ. Bạn phải tuân thủ đúng trật tự biến đổi để đảm bảo tính chính xác cho biểu thức cuối cùng.
Công thức đạo hàm hàm hợp
Hàm hợp thường xuất hiện dưới dạng một hàm số nằm lồng bên trong một hàm số khác, tạo nên một cấu trúc phân tầng phức tạp đòi hỏi kỹ năng xử lý tinh tế. Bạn cần thực hiện phép tính từ lớp vỏ bên ngoài vào đến phần lõi bên trong để không bỏ sót bất kỳ thành phần nào.
Quy tắc lũy thừa
Đối với các hàm số chứa biến số ở phần cơ số và hằng số ở phần mũ, chúng ta áp dụng phương pháp hạ bậc kết hợp với việc nhân hệ số tương ứng. Đây là dạng bài tập phổ biến nhất mà bất kỳ ai mới bắt đầu làm quen với giải tích cũng đều phải thực hiện thuần thục.

Ứng dụng thực tế của đạo hàm trong đời sống hàng ngày
Khái niệm đạo hàm không chỉ tồn tại trên những trang giấy trắng hay bảng đen mà còn len lỏi vào mọi ngóc ngách của các ngành khoa học và kinh tế hiện đại. Dưới đây là những ví dụ tiêu biểu cho thấy sức mạnh của việc tính toán sự biến thiên trong thực tế:
- Trong lĩnh vực vật lý học, phép toán này cho phép chúng ta xác định vận tốc tức thời của một vật thể đang chuyển động khi biết được phương trình quãng đường của nó.
- Các chuyên gia kinh tế sử dụng công cụ này để tính toán chi phí biên, từ đó đưa ra quyết định tối ưu hóa lợi nhuận cho các doanh nghiệp quy mô lớn.
- Trong kiến trúc và xây dựng, đạo hàm giúp tính toán độ cong và sức chịu tải của các vòm cầu, đảm bảo an toàn tuyệt đối cho các công trình hạ tầng.
- Ngành hóa học ứng dụng phép biến thiên để theo dõi tốc độ phản ứng giữa các chất, giúp kiểm soát quy trình sản xuất dược phẩm và vật liệu mới.
- Các thuật toán trí tuệ nhân tạo ngày nay cũng dựa vào việc tính toán gradient, một dạng mở rộng của khái niệm này, để tối ưu hóa khả năng học tập của máy tính.
- Ngay cả trong y học, việc dự đoán sự lây lan của dịch bệnh hoặc sự phát triển của khối u cũng cần đến sự hỗ trợ của các phương trình vi phân liên quan.
- Trong khí tượng thủy văn, các nhà khoa học dùng nó để phân tích sự thay đổi áp suất không khí, từ đó đưa ra những dự báo thời tiết chính xác cho cộng đồng.
Bảng công thức đạo hàm của các hàm số lượng giác
Trong đạo hàm, các hàm số như sin, cos hay tan thường gây ra không ít khó khăn cho người học do tính chất tuần hoàn và các biến đổi hình học đặc thù của chúng. Việc hệ thống hóa các kết quả biến đổi của chúng vào một bảng biểu sẽ giúp quá trình tra cứu và ghi nhớ trở nên thuận tiện hơn rất nhiều.
| Loại hàm số | Biểu thức gốc | Kết quả sau khi biến đổi |
| Hàm số Sin | y = sin(x) | y’ = cos(x) |
| Hàm số Cos | y = cos(x) | y’ = -sin(x) |
| Hàm số Tan | y = tan(x) | y’ = 1/cos²(x) |
| Hàm số Cot | y = cot(x) | y’ = -1/sin²(x) |
Biến đổi hàm sin
Kết quả của việc tính toán tốc độ thay đổi trong đạo hàm của hàm sin chính là hàm cosin, một sự chuyển đổi nhịp nhàng giữa hai thực thể lượng giác cơ bản. Điều này phản ánh mối quan hệ mật thiết giữa các cạnh trong một tam giác vuông khi góc xoay thay đổi liên tục.
Lưu ý về hàm cos
Một điểm cần đặc biệt chú ý khi xử lý hàm cos trong đạo hàm chính là sự xuất hiện của dấu âm trong kết quả cuối cùng, điều này thường khiến nhiều người nhầm lẫn. Dấu trừ này biểu thị cho việc giá trị của hàm số đang giảm dần trong một khoảng xác định của vòng tròn lượng giác.
Phép toán với hàm tan
Hàm tan có sự biến đổi phức tạp hơn khi kết quả của đạo hàm dẫn đến một biểu thức chứa bình phương của hàm cos nằm ở dưới mẫu số. Điều này liên quan đến việc hàm tan vốn dĩ là tỉ số giữa sin và cos, nên khi biến đổi sẽ áp dụng quy tắc thương.
Kết luận
Đạo hàm không chỉ là những con số khô khan mà còn là chìa khóa vạn năng giải mã sự vận động của thế giới xung quanh chúng ta một cách chính xác. Hy vọng bài viết đã cung cấp cho bạn cái nhìn thấu đáo để tự tin đối mặt với mọi bài kiểm tra khó nhằn nhất trong chương trình học. Hãy tiếp tục theo dõi và cập nhật những thông tin tri thức mới nhất từ thương hiệu SevenAM.