Hình bình hành hiện thân như một trong những cấu trúc hình học phổ biến nhất mà chúng ta thường xuyên bắt gặp trong các bản thiết kế kiến trúc hiện đại. Những quy định về tính chất và các công thức tính toán liên quan đến hình khối này luôn là nền tảng tri thức không thể thiếu đối với bất kỳ ai đang theo đuổi khối ngành kỹ thuật. Hãy cùng trải nghiệm góc nhìn mới mẻ về các định nghĩa hình học cơ bản thông qua lăng kính sáng tạo từ thương hiệu SevenAM.
Thế giới kỳ diệu của hình bình hành và bản chất hình học
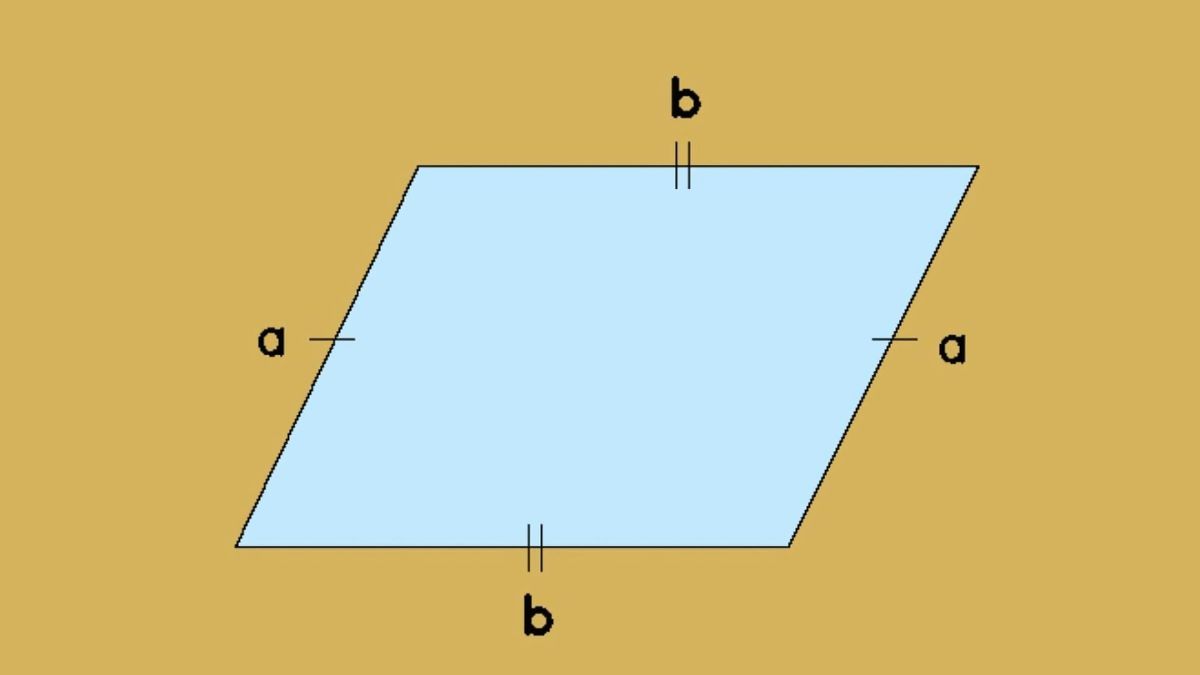
Khái niệm về một tứ giác có các cặp cạnh đối diện luôn duy trì khoảng cách không đổi và song song tuyệt đối chính là định nghĩa cơ bản nhất mà chúng ta cần ghi nhớ. Trong không gian hai chiều, thực thể này không chỉ đơn thuần là những đường thẳng nối liền mà còn chứa đựng những quy luật đối xứng tâm vô cùng thú vị.
Xét về mặt bản chất, một hình bình hành sẽ bộc lộ toàn bộ đặc trưng thông qua việc các góc đối diện luôn có số đo bằng nhau một cách tuyệt đối. Nếu bạn thực hiện phép xoay khối hình này một góc một trăm tám mươi độ quanh giao điểm của hai đường chéo, toàn bộ hình dáng sẽ trùng khít hoàn toàn với vị trí ban đầu.
Khi nghiên cứu sâu hơn, ta thấy rằng diện tích bao phủ bởi khối hình này phụ thuộc trực tiếp vào độ dài của cạnh đáy và khoảng cách vuông góc từ đáy đến đỉnh đối diện. Việc nắm vững các đặc điểm nhận dạng sẽ giúp bạn dễ dàng giải quyết các bài toán từ cơ bản đến phức tạp trong chương trình giáo dục phổ thông.
Những công thức tính toán thông số hình bình hành
Hệ thống các biểu thức toán học dùng để đo lường các giá trị định lượng của khối hình này vô cùng logic và dễ dàng áp dụng. Việc xác định chính xác các số liệu sẽ giúp quá trình thiết kế hoặc giải toán trở nên thuận tiện và đạt độ chính xác cao hơn.
Tính chu vi tứ giác
Phép tính tổng độ dài các cạnh bao quanh khối hình được thực hiện bằng cách lấy hai lần tổng của hai cạnh kề nhau. Bạn chỉ cần xác định số đo của hai cạnh khác nhau rồi nhân đôi kết quả đó để ra thông số cuối cùng.
Đo lường diện tích bề mặt
Để tìm ra giá trị không gian bên trong, bạn thực hiện phép nhân giữa độ dài một cạnh đáy với chiều cao tương ứng được hạ từ đỉnh. Lưu ý rằng chiều cao phải là đoạn thẳng vuông góc nối giữa hai cạnh song song chứ không phải là độ dài cạnh bên.
Độ dài cạnh hình bình hành
Trong trường hợp đã biết diện tích và chiều cao, việc tìm kiếm thông số độ dài cạnh đáy được thực hiện bằng phép tính chia đơn giản. Đây là cách thức thường dùng trong các bài toán ngược nhằm kiểm tra tư duy logic của người học trong môi trường giáo dục.
Đường chéo và giao điểm
Hai đoạn thẳng nối các đỉnh đối diện nhau luôn có đặc tính cắt nhau tại vị trí chính giữa của mỗi đường thẳng đó. Điều này tạo ra một sự cân bằng tuyệt đối về mặt không gian, chia khối hình thành những tam giác có diện tích hoàn toàn tương đương nhau.

Phương pháp xác định cấu trúc hình bình hành nhanh chóng
Để nhận biết một tứ giác có phải là cấu trúc đặc biệt này hay không, chúng ta cần dựa trên một số tiêu chuẩn định tính cụ thể. Dưới đây là những dấu hiệu nhận biết quan trọng nhất mà bạn cần lưu tâm khi thực hiện các bài kiểm tra hoặc ứng dụng thực tế:
- Tứ giác có hai cặp cạnh đối diện song song với nhau được coi là một hình bình hành chuẩn mực theo đúng định nghĩa.
- Nếu một hình sở hữu các cặp cạnh đối diện có chiều dài bằng nhau thì chắc chắn nó sẽ thuộc vào nhóm hình này.
- Chỉ cần một cặp cạnh đối diện vừa đảm bảo tính chất song song vừa có độ dài bằng nhau là đủ điều kiện xác nhận.
- Sự bằng nhau của các góc đối diện trong một tứ giác cũng là một minh chứng xác thực cho cấu trúc hình bình hành mà bạn đang tìm kiếm.
- Đặc điểm hai đường chéo cắt nhau ngay tại trung điểm của mỗi đường là dấu hiệu không thể sai lệch trong các bài toán chứng minh.
Để có cái nhìn trực quan hơn về sự khác biệt giữa các hình khối, bạn có thể tham khảo bảng so sánh dưới đây:
| Loại hình học | Cặp cạnh đối song song | Các cạnh bằng nhau | Các góc bằng nhau |
| Hình bình hành | Có (2 cặp) | Chỉ các cặp đối diện | Chỉ các cặp đối diện |
| Hình chữ nhật | Có (2 cặp) | Chỉ các cặp đối diện | Tất cả (90 độ) |
| Hình thoi | Có (2 cặp) | Tất cả 4 cạnh | Chỉ các cặp đối diện |
| Hình vuông | Có (2 cặp) | Tất cả 4 cạnh | Tất cả (90 độ) |
Việc đối chiếu các thông số trên bảng giúp chúng ta thấy rằng hình bình hành chính là “cha đẻ” của nhiều hình khối đặc biệt khác. Khi chúng ta thêm các điều kiện về góc hoặc độ dài cạnh, cấu trúc này sẽ biến đổi thành những hình có tính đối xứng cao hơn.
Giá trị thực tiễn từ mô hình hình bình hành đời sống
Không chỉ dừng lại ở những trang sách vở, cấu trúc này hiện diện mạnh mẽ trong mọi ngóc ngách của đời sống và các ngành công nghiệp. Việc ứng dụng các đặc tính của hình bình hành mang lại sự tối ưu về cả thẩm mỹ lẫn công năng sử dụng cho các sản phẩm nhân tạo.
Kiến trúc và xây dựng
Các kiến trúc sư thường tận dụng tính chất biến thiên góc của khối hình này để tạo ra những tòa nhà có hình dáng độc đáo và bắt mắt. Những mái nhà hay vách ngăn mang phong cách hiện đại thường xuyên sử dụng khung hình này để tạo cảm giác chuyển động và sự thanh thoát cho công trình.
Cơ khí và chuyển động
Trong lĩnh vực chế tạo máy, cơ cấu đòn bẩy dựa trên nguyên lý của hình bình hành giúp duy trì sự song song của các bộ phận khi di chuyển. Bạn có thể dễ dàng quan sát thấy điều này ở các cần cẩu nâng hạ hoặc các giá đỡ màn hình máy tính có khả năng điều chỉnh linh hoạt.
Thiết kế đồ họa
Các chuyên gia sáng tạo thường dùng khối hình này để tạo ra hiệu ứng chiều sâu và phối cảnh trong các tác phẩm nghệ thuật kỹ thuật số. Sự nghiêng nhẹ của các cạnh tạo ra cảm giác về không gian ba chiều, giúp các logo hoặc biểu tượng trở nên sinh động và có sức hút hơn đối với người xem.
Kết luận
Hình bình hành là một mảnh ghép không thể thiếu trong bức tranh tổng thể của toán học và các ứng dụng thực tiễn đa dạng ngày nay. Hy vọng những thông tin chuẩn xác về tính chất, công thức và dấu hiệu nhận biết đã giúp bạn củng cố kiến thức một cách vững chãi nhất. Hãy tiếp tục khám phá thêm nhiều điều thú vị và áp dụng chúng vào cuộc sống cùng với sự đồng hành của SevenAM.