Bảng nguyên hàm là tập hợp các công thức giúp bạn tìm nguyên hàm nhanh mà không phải suy luận lại từ đầu. Khi nắm chắc các nhóm công thức cơ bản, bạn sẽ rút ngắn thời gian làm bài và hạn chế sai sót. Điều quan trọng là luôn nhớ cộng thêm hằng số C và kiểm tra điều kiện xác định trước khi áp dụng.
Bảng nguyên hàm cơ bản cần nhớ
Nguyên hàm của hàm lũy thừa
Với m ≠ -1, ta có ∫xm dx = x(m+1)/(m+1) + C. Công thức này xuất hiện rất nhiều trong các bài toán biến đổi biểu thức và tính tích phân cơ bản. Khi gặp dạng có hệ số k nhân bên trong, bạn thường cần đưa về dạng “chuẩn” để áp dụng gọn hơn.
Nguyên hàm của hằng số và tổng – hiệu
Nếu a là hằng số thì ∫a dx = ax + C. Ngoài ra, nguyên hàm có tính tuyến tính nên ∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx. Nhờ tính chất này, bạn có thể tách biểu thức dài thành nhiều phần nhỏ để xử lý nhanh và ít nhầm dấu.
Nguyên hàm dạng 1/x
Với x ≠ 0, ∫(1/x) dx = ln|x| + C. Dạng này thường bị nhầm với lũy thừa m = -1, nên bạn cần nhận diện riêng để không áp dụng sai công thức lũy thừa. Khi trong bài có dạng 1/(ax+b), bạn sẽ cần thêm bước đổi biến đơn giản.
Bảng nguyên hàm lượng giác hay gặp
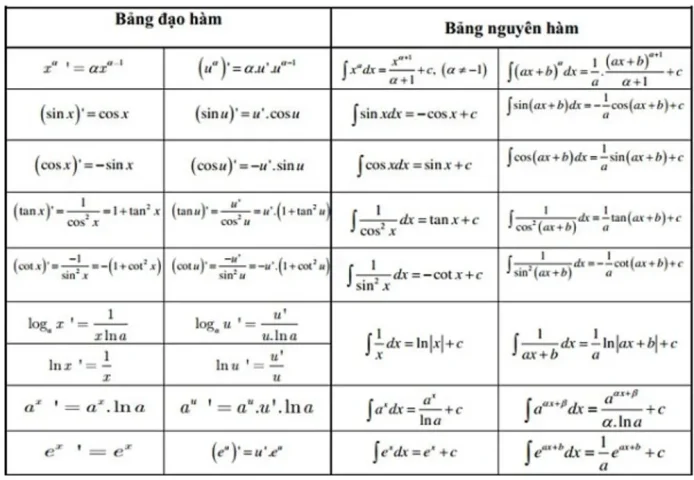
Nhóm sin, cos cơ bản
Ta có ∫sin x dx = -cos x + C và ∫cos x dx = sin x + C. Đây là hai công thức nền tảng, dùng liên tục trong bài tập trắc nghiệm lẫn tự luận. Bạn nên luyện phản xạ dấu “trừ” ở nguyên hàm của sin để tránh sai sót đáng tiếc.
Nhóm tan, cot và các dạng liên quan
Với điều kiện xác định phù hợp, ∫tan x dx = -ln|cos x| + C và ∫cot x dx = ln|sin x| + C. Những công thức này rất hữu ích khi rút gọn biểu thức về tỉ số sin/cos. Nếu bạn thấy dạng sec2 x hoặc csc2 x, hãy liên tưởng ngay đến đạo hàm của tan và cot để tìm nguyên hàm nhanh.
Nhóm sec2 và csc2
Ta có ∫sec2 x dx = tan x + C và ∫csc2 x dx = -cot x + C. Các dạng này thường xuất hiện khi đề bài cho biểu thức đã biến đổi sẵn hoặc sau bước dùng công thức lượng giác. Khi luyện tập, bạn nên kiểm tra lại bằng cách lấy đạo hàm kết quả để chắc chắn dấu đúng.
Bảng nguyên hàm hàm mũ và logarit

Nguyên hàm của ex và ax
Ta có ∫ex dx = ex + C, còn với a > 0, a ≠ 1 thì ∫ax dx = ax/ln a + C. Điểm hay nhầm là thiếu “/ln a” khi ax không phải ex. Nếu trong mũ có kx, bạn cần chia thêm cho k để bù lại hệ số bên trong.
Nguyên hàm của ln x (cơ bản)
Với x > 0, ∫ln x dx = x ln x – x + C. Công thức này thường dùng khi gặp bài cần tích phân từng phần hoặc nhận diện trực tiếp từ bảng công thức. Bạn nên ghi nhớ theo cặp: đạo hàm của x ln x là ln x + 1, từ đó suy ra kết quả dễ hơn.
Bảng nguyên hàm dạng “ax + b” thường xuyên xuất hiện
Dạng 1/(ax+b)
Với ax+b ≠ 0, ∫1/(ax+b) dx = (1/a)ln|ax+b| + C. Đây là dạng đổi biến nhanh, thường chỉ cần đặt t = ax+b rồi dt = a dx. Khi a âm hoặc phân số, hãy cẩn thận hệ số 1/a để không bị lệch kết quả.
Dạng (ax+b)^n
Với n ≠ -1, ∫(ax+b)n dx = (ax+b)(n+1)/(a(n+1)) + C. Dạng này là “bản nâng cấp” của công thức lũy thừa, kết hợp thêm hệ số a bên trong. Bạn nên kiểm tra lại bằng cách đạo hàm để thấy hệ số a nhân lên đúng như ban đầu.
Mẹo học nhanh và dùng công thức hiệu quả

Nhóm hóa để nhớ công thức
Bạn sẽ nhớ lâu hơn nếu chia công thức theo nhóm: lũy thừa, 1/x, lượng giác, mũ–log. Khi luyện, hãy tự viết lại mỗi nhóm theo dạng “đạo hàm ↔ nguyên hàm” để tạo phản xạ hai chiều. Cách học này giúp bạn không chỉ thuộc mà còn hiểu vì sao công thức đúng.
Luôn kiểm tra hằng số C và điều kiện xác định
Nhiều bạn làm đúng gần hết nhưng quên +C, khiến bài tự luận mất điểm đáng tiếc. Với các biểu thức có log, bạn cần nhớ dấu giá trị tuyệt đối và điều kiện của biến. Thói quen kiểm tra nhanh ở cuối sẽ giúp bạn tránh các lỗi nhỏ nhưng “đắt giá”.
Khi nào nên đổi biến và khi nào nên rút gọn trước
Nếu biểu thức có dạng “hàm của ax+b” hoặc “hàm của kx”, đổi biến thường là con đường nhanh nhất. Nếu biểu thức là tổng nhiều hạng, rút gọn hoặc tách nhỏ sẽ hiệu quả hơn trước khi áp dụng công thức. Bạn nên thử nhìn cấu trúc trong 5–10 giây đầu để chọn chiến lược phù hợp.
Bài tập mẫu áp dụng nhanh
Ví dụ 1: Dạng lũy thừa
Tính ∫(3x^2 – 4x + 1) dx. Bạn tách từng hạng và áp dụng công thức nguyên hàm lũy thừa cho mỗi phần để ra kết quả. Cuối cùng, bạn nhớ cộng hằng số C và có thể đạo hàm lại để kiểm tra.
Ví dụ 2: Dạng 1/(ax+b)
Tính ∫ 2/(2x-1) dx. Bạn nhận ra đây là dạng 1/(ax+b) nên kết quả là 2 * (1/2)ln|2x-1| + C, tức ln|2x-1| + C. Bài dạng này rất hay xuất hiện trong trắc nghiệm vì làm nhanh nếu nhận diện đúng.
Ví dụ 3: Dạng mũ cơ bản
Tính ∫ 5e^(5x) dx. Bạn dùng công thức mũ và chia cho hệ số bên trong để được e^(5x) + C. Nếu bạn quên chia cho 5, kết quả sẽ bị sai ngay khi kiểm tra đạo hàm.
Lỗi sai phổ biến khi học nguyên hàm
Nhầm dấu ở lượng giác
Nhiều bạn nhầm ∫sin x dx thành cos x + C, trong khi đúng là -cos x + C. Lỗi này có thể tránh bằng mẹo: đạo hàm cos x là -sin x nên muốn ra sin x thì phải là -cos x. Khi làm bài, bạn chỉ cần kiểm tra ngược 1 bước là phát hiện ngay.
Dùng sai công thức với m = -1
Khi gặp x^-1, bạn không được áp dụng công thức lũy thừa thông thường. Lúc này công thức đúng là ln|x| + C, và đây là trường hợp đặc biệt cần nhớ riêng. Nếu bạn thuộc kỹ điểm này, bạn sẽ tránh được một trong những lỗi phổ biến nhất cùng sevenam.
Kết luận
Khi nắm chắc Bảng nguyên hàm, bạn sẽ làm chủ phần kiến thức nền của tích phân và các bài toán ứng dụng. Hãy học theo nhóm, luyện phản xạ kiểm tra đạo hàm và luôn nhớ hằng số C để hạn chế sai sót. Chỉ cần luyện đều, bạn sẽ thấy tốc độ xử lý bài tăng lên rõ rệt và tự tin hơn khi vào phòng thi.