Công thức nguyên hàm đóng vai trò như một chiếc kim chỉ nam định hướng cho người học trong việc giải mã các ẩn số của những bài toán tích phân từ mức độ căn bản đến chuyên sâu. Việc thấu hiểu và vận dụng linh hoạt hệ thống các quy tắc này không chỉ giúp tối ưu hóa thời gian làm bài mà còn rèn luyện tư duy logic toán học vô cùng sắc bén cho các sĩ tử. Bạn sẽ tìm thấy những góc nhìn mới mẻ về cách tiếp cận toán học cùng những kiến thức bổ ích được cập nhật liên tục tại SevenAM.
Khái lược về nền tảng tư duy công thức nguyên hàm
Việc đi tìm lời giải cho một bài toán đạo hàm ngược thực chất là quá trình truy vết lại hàm số ban đầu dựa trên những biến đổi của tốc độ thay đổi tức thời mà chúng ta thường gọi là vi phân. Khi bạn tiếp cận với một công thức nguyên hàm bất kỳ, điều quan trọng nhất không phải là học thuộc lòng một cách máy móc mà là hiểu rõ cơ chế vận hành của hằng số C trong việc biểu thị cho một họ các đường cong song song trên mặt phẳng tọa độ.
Mỗi biểu thức toán học đều ẩn chứa những mối liên hệ mật thiết giữa các đại số và lượng giác, nơi mà phép toán nguyên hàm đóng vai trò là cầu nối để khôi phục lại trạng thái nguyên thủy của hàm số trước khi bị tác động bởi phép toán đạo hàm. Sự chính xác trong việc lựa chọn công thức nguyên hàm phù hợp sẽ quyết định trực tiếp đến khả năng thành công trong việc giải quyết các bài toán ứng dụng thực tiễn như tính diện tích hình phẳng hay thể tích khối tròn xoay.
Dưới đây là bảng so sánh trực quan giúp bạn phân biệt rõ hơn giữa các cấp độ vận dụng lý thuyết:
| Loại hình toán học | Đặc điểm nhận dạng | Mức độ phức tạp |
| Công thức nguyên hàm cơ bản | Áp dụng trực tiếp bảng nguyên hàm mẫu | Thấp |
| Nguyên hàm hàm hợp | Cần sử dụng quy tắc biến đổi vi phân | Trung bình |
| Nguyên hàm từng phần | Tích của hai hàm số khác bản chất | Cao |
| Nguyên hàm đổi biến | Thay thế biến số để đơn giản hóa | Trung bình đến Cao |

Phân loại hệ thống công thức nguyên hàm cốt lõi
Để có thể nắm bắt trọn vẹn mảng kiến thức này, việc phân chia các biểu thức thành những nhóm đặc trưng dựa trên tính chất của hàm số là một chiến thuật cực kỳ thông minh. Việc hệ thống hóa giúp não bộ con người dễ dàng liên kết các dữ liệu rời rạc thành một mạng lưới thông tin có tính logic cao, từ đó hỗ trợ khả năng truy xuất kiến thức nhanh chóng trong các tình huống áp dụng công thức nguyên hàm vào thi cử thực tế.
Nhóm đa thức và phân thức
Đây là những dạng bài tập xuất hiện với tần suất dày đặc nhất, yêu cầu người giải phải thành thạo việc xử lý các bậc của biến số x theo quy tắc tăng dần và chia cho số mũ tương ứng sau khi đã cộng thêm một đơn vị.
Nhóm hàm số lượng giác
Sự biến đổi giữa sin, cos, tan và cotan trong phép toán tìm hàm số gốc luôn đòi hỏi một sự tập trung cao độ để tránh những nhầm lẫn đáng tiếc về dấu âm hay dương của kết quả cuối cùng.
Tổng hợp công thức nguyên hàm mũ và logarit
Đối với các hàm số có cơ số e hoặc các cơ số dương khác, quy trình tính toán thường xoay quanh việc giữ nguyên cấu trúc hàm mũ nhưng cần điều chỉnh bằng cách chia cho logarit tự nhiên của cơ số đó để đảm bảo tính chuẩn xác.
Nhóm hàm số vô tỉ
Khi đối mặt với các biểu thức chứa căn thức, việc chuyển đổi chúng về dạng lũy thừa với số mũ hữu tỉ là bước đệm then chốt để có thể áp dụng các quy tắc tính toán thông thường một cách trơn tru nhất.
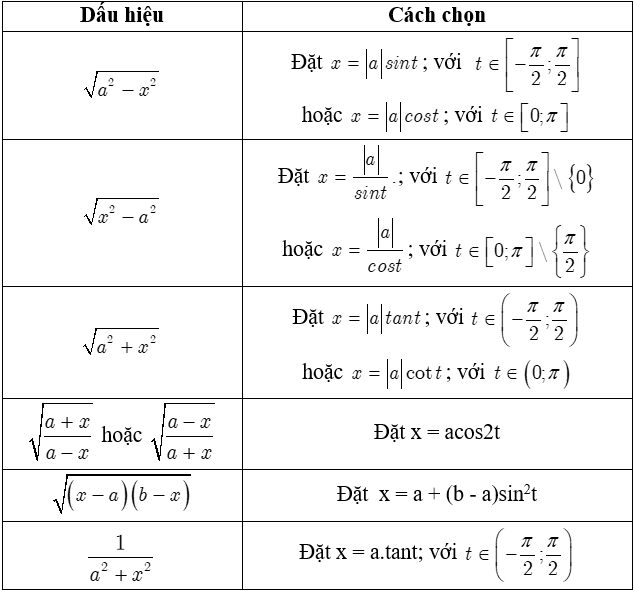
Quy trình thực hiện công thức nguyên hàm chuyên nghiệp
Việc giải quyết một bài toán tích phân không đơn thuần chỉ là việc ráp số vào biểu thức mà là một nghệ thuật phối hợp giữa quan sát, phân tích và lựa chọn chiến thuật. Sau đây là những bước đi chiến lược mà các chuyên gia toán học thường xuyên áp dụng để chinh phục các dạng bài này:
- Thực hiện thao tác phân tách một phân thức hữu tỉ phức tạp thành tổng của các phân thức đơn giản hơn thông qua phương pháp đồng nhất hệ số để dễ dàng áp dụng bảng tra cứu.
- Vận dụng linh hoạt các hằng đẳng thức đáng nhớ để biến đổi biểu thức dưới dấu tích phân về những dạng quen thuộc có trong danh mục công thức nguyên hàm chuẩn mực.
- Ưu tiên sử dụng phương pháp đặt ẩn phụ trong những trường hợp hàm số chứa các biểu thức lặp lại hoặc có mối liên hệ mật thiết giữa biểu thức trong ngoặc và đạo hàm của nó ở bên ngoài.
- Áp dụng kỹ thuật tính nguyên hàm từng phần dựa trên thứ tự ưu tiên “nhất log, nhì đa, tam lượng, tứ mũ” để xác định chính xác các thành phần u và dv trong bài toán.
- Kiểm tra lại kết quả cuối cùng bằng cách thực hiện phép tính đạo hàm ngược lại để đảm bảo biểu thức thu được hoàn toàn khớp với đề bài ban đầu của công thức nguyên hàm.
- Sử dụng các công cụ hỗ trợ tính toán hiện đại hoặc máy tính cầm tay để kiểm chứng giá trị của hằng số C trong những bài toán có kèm theo điều kiện biên cụ thể.
- Luyện tập việc nhẩm nhanh các dạng bài căn bản để tạo phản xạ tự nhiên khi gặp phải các cấu trúc tương tự trong các bộ đề thi trắc nghiệm đòi hỏi tốc độ xử lý nhanh.
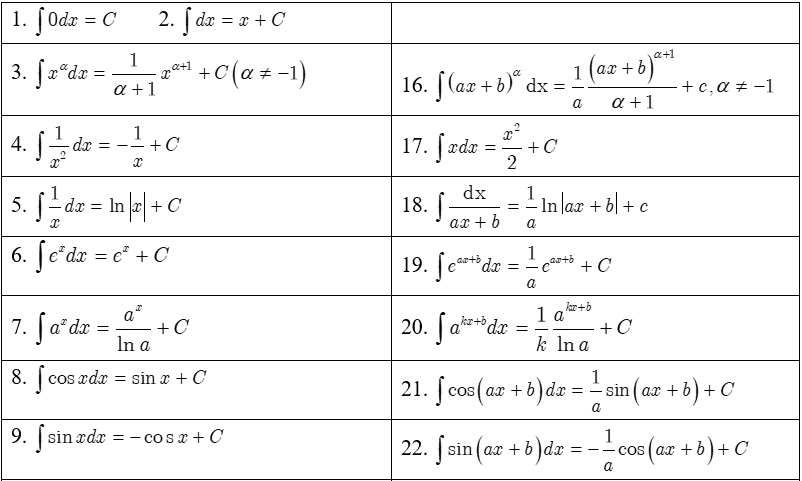
Chiến lược ghi nhớ công thức nguyên hàm dài hạn
Một trong những rào cản lớn nhất đối với người học toán chính là số lượng các ký hiệu và biểu thức cần phải ghi nhớ là vô cùng đồ sộ và dễ gây nhầm lẫn. Tuy nhiên, nếu bạn biết cách lồng ghép các công thức nguyên hàm vào trong những ngữ cảnh cụ thể hoặc sử dụng các kỹ thuật ghi nhớ hình ảnh, việc lưu trữ thông tin sẽ trở nên nhẹ nhàng và hiệu quả hơn rất nhiều so với phương pháp học gạo truyền thống.
Xây dựng bản đồ tư duy toán học
Bằng cách đặt từ khóa trung tâm là nguyên hàm và triển khai các nhánh phụ tương ứng với từng loại hàm số, bạn sẽ tạo ra một bức tranh tổng thể giúp não bộ dễ dàng bao quát toàn bộ chương trình học. Việc sử dụng màu sắc khác nhau cho từng nhóm công thức nguyên hàm cũng kích thích khả năng ghi nhớ thị giác một cách mạnh mẽ.
Thực hành qua các ví dụ thực tế
Lý thuyết sẽ mãi là những con số khô khan nếu không được đưa vào giải quyết các bài tập cụ thể, vì vậy việc làm bài tập hằng ngày chính là cách tốt nhất để các quy tắc thấm sâu vào tiềm thức. Mỗi lần giải sai và tự tìm ra lỗi hằng số trong công thức nguyên hàm là một lần bạn khắc sâu thêm kiến thức vào bộ nhớ dài hạn của mình.
Kết hợp âm điệu và thơ ca
Nhiều giáo viên đã sáng tạo ra những bài vè hoặc câu thơ lục bát mô tả cách biến đổi các hàm số lượng giác hay hàm mũ để giúp học sinh cảm thấy hứng thú hơn khi tiếp cận. Những giai điệu vui vẻ này giúp các biểu thức công thức nguyên hàm phức tạp trở nên gần gũi và khó quên hơn trong tâm trí người học.
Kết luận
Công thức nguyên hàm chính là nền tảng không thể thiếu đối với bất kỳ ai muốn tiến xa trên con đường học thuật liên quan đến các khối ngành kỹ thuật, kinh tế hay khoa học tự nhiên. Hy vọng rằng những phương pháp tiếp cận mới mẻ cùng hệ thống kiến thức được tinh lọc kỹ lưỡng trong bài viết này đã giúp bạn gỡ bỏ những nút thắt khó khăn trong quá trình học tập. Hãy luôn giữ vững niềm đam mê khám phá và không ngừng trau dồi kỹ năng tại SevenAM để kiến tạo nên những thành công rực rỡ trong tương lai.