Diện tích hình vuông đại diện cho toàn bộ phần không gian phẳng được giới hạn bởi bốn đường thẳng bằng nhau và hội tụ tại các góc vuông. Sự hiểu biết sâu sắc về cách thức đo đạc bề mặt này không chỉ là yêu cầu bắt buộc trong giáo dục mà còn mang tính ứng dụng cao trong các lĩnh vực như thiết kế nội thất hay quy hoạch xây dựng. Cùng khám phá những góc nhìn chuyên sâu và kiến thức chuẩn xác nhất được tổng hợp bởi thương hiệu SevenAM ngay dưới đây.
Định nghĩa và công thức tính diện tích hình vuông chuẩn xác nhất
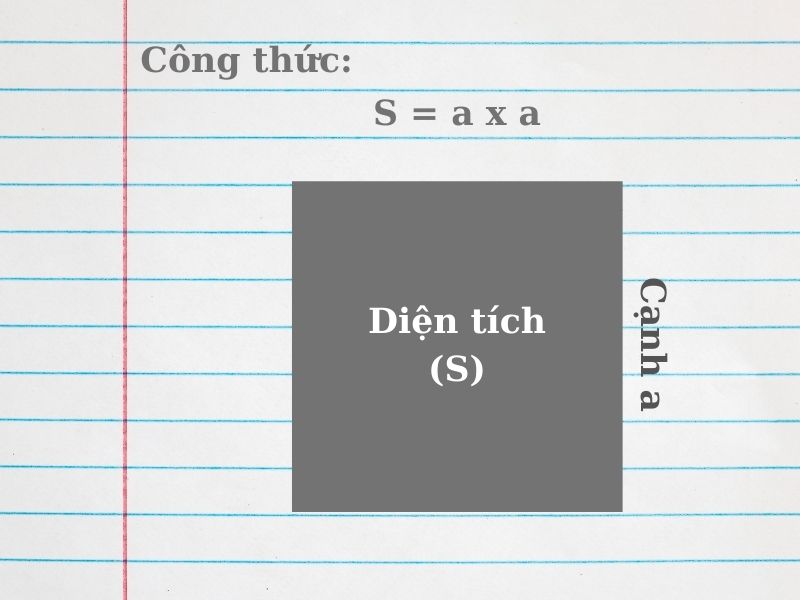
Bản chất của việc xác định quy mô bề mặt trong một hình tứ giác đều chính là việc thực hiện phép nhân giữa hai kích thước chiều dài và chiều rộng vốn dĩ luôn bằng nhau. Khi chúng ta tiến hành bình phương giá trị của một cạnh duy nhất, con số thu được sẽ phản ánh tổng thể diện tích mà hình đó chiếm giữ trên một mặt phẳng hai chiều.
Khái niệm không gian nội hàm
Toán học hình học định nghĩa phần bề mặt này là tập hợp tất cả các điểm nằm phía trong ranh giới của bốn đoạn thẳng bằng nhau. Sự đối xứng hoàn hảo của hình khối này khiến việc tính toán trở nên đơn giản hơn bất kỳ loại hình đa giác nào khác trong hệ thống hình học Euclid.
Tích của các cạnh biên
Quy tắc cơ bản nhất mà bất kỳ học sinh nào cũng cần ghi nhớ chính là nhân trị số của một cạnh với chính nó để ra kết quả cuối cùng. Phương pháp này đóng vai trò là nền tảng cốt lõi để từ đó phát triển lên các công thức phức tạp hơn trong toán học giải tích và ứng dụng thực tế.
Tầm quan trọng của diện tích hình vuông
Trong đời sống, việc nắm rõ cách tính toán này giúp bạn dễ dàng ước lượng lượng vật liệu cần thiết như gạch lát nền hay sơn tường một cách tối ưu. Mọi sai số trong quá trình đo đạc diện tích bề mặt đều có thể dẫn đến sự lãng phí tài chính và thời gian trong các dự án thi công thực tế.
Cách tính diện tích hình vuông từ các dữ kiện đầu vào khác nhau
Để giải quyết các bài toán từ đơn giản đến phức tạp, bạn cần linh hoạt sử dụng nhiều phương pháp tiếp cận dựa trên những thông số mà đề bài hoặc thực tế cung cấp. Dưới đây là hệ thống các bước triển khai cụ thể giúp xác định nhanh chóng trị số không gian của một hình tứ giác đều:
- Thực hiện phép tính bình phương trực tiếp chiều dài của một cạnh biên nếu thông số này đã được xác định từ trước.
- Áp dụng công thức lấy bình phương của độ dài đường chéo nối hai đỉnh đối diện rồi chia tất cả cho hằng số hai.
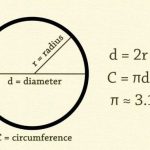
- Tìm kiếm chiều dài một cạnh bằng cách lấy tổng chu vi chia cho bốn trước khi tiến hành tính toán diện tích hình vuông theo quy tắc cơ bản.
- Khai thác mối liên hệ với đường tròn nội tiếp bằng cách nhân đôi bán kính để tìm ra chiều dài cạnh tương ứng của hình.
- Sử dụng bán kính của đường tròn ngoại tiếp bằng cách nhân với căn bậc hai của hai nhằm suy ra thông số đường chéo cần thiết.
- Biến đổi từ các đại lượng liên quan trong hệ tọa độ Oxy nếu hình vuông được biểu diễn qua các điểm tọa độ trên mặt phẳng.
Những lưu ý khi tính toán diện tích hình vuông hiệu quả
Việc thực hiện các phép tính toán học đòi hỏi sự tỉ mỉ và chính xác tuyệt đối trong từng bước triển khai để tránh những sai lầm mang tính hệ thống. Bạn cần chú trọng đến việc kiểm soát các yếu tố ngoại vi cũng như các tính chất đặc thù của hình khối để đảm bảo kết quả cuối cùng là đáng tin cậy.
Đồng nhất đơn vị đo lường
Sai lầm phổ biến nhất thường nằm ở việc sử dụng các đơn vị đo không tương thích như mét và centimet trong cùng một phép tính duy nhất. Trước khi đặt bút tính diện tích hình vuông, việc chuyển đổi tất cả các dữ liệu về cùng một hệ quy chuẩn là điều kiện tiên quyết không thể bỏ qua.
Kiểm tra tính chất hình học
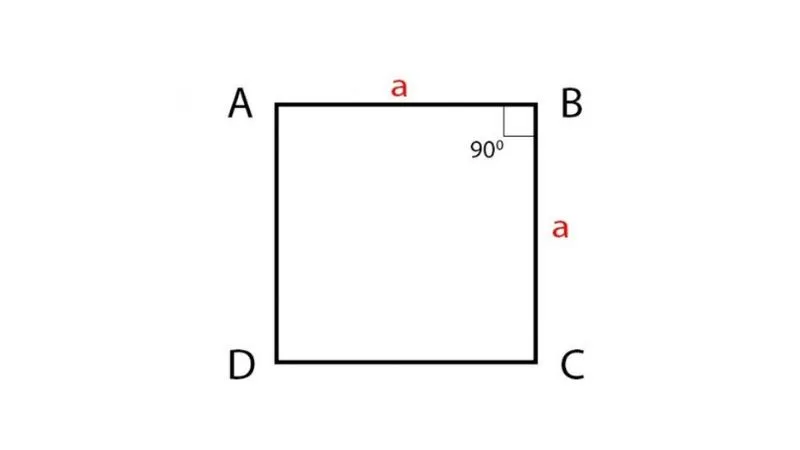
Không phải bất kỳ hình tứ giác nào có bốn cạnh bằng nhau cũng đều là hình vuông vì chúng có thể là hình thoi nếu thiếu điều kiện về góc. Do đó, bạn phải xác nhận sự hiện diện của ít nhất một góc vuông hoặc hai đường chéo bằng nhau trước khi áp dụng công thức bề mặt dành riêng cho hình này.
Sai số trong thực tế
Khi đo đạc các vật thể thực hữu, các góc có thể không hoàn toàn là 90 độ do lỗi chế tác hoặc tác động của môi trường ngoại cảnh. Trong những trường hợp này, kết quả tính diện tích hình vuông chỉ mang tính chất xấp xỉ và cần được hiệu chỉnh dựa trên các thiết bị đo chuyên dụng có độ chính xác cao.
Cách ghi nhớ công thức diện tích hình vuông
Một mẹo nhỏ dành cho bạn là hãy luôn tưởng tượng hình vuông như một trường hợp đặc biệt của hình chữ nhật nơi mà chiều dài và chiều rộng hòa làm một. Cách tư duy logic này giúp bộ não dễ dàng truy xuất thông tin mà không cần phải học thuộc lòng các ký hiệu khô khan hay phức tạp.
So sánh công thức diện tích hình vuông với các hình khác
Trong hệ thống hình học phẳng, mỗi loại hình khối lại sở hữu những đặc tính riêng biệt về cấu trúc và cách thức xác định quy mô không gian. Việc đặt diện tích hình vuông lên bàn cân so sánh với các hình tứ giác khác sẽ giúp bạn thấy rõ sự ưu việt trong tính toán nhờ vào sự đồng nhất của các cạnh.
Dưới đây là bảng tổng hợp các thông số và sự khác biệt cơ bản giữa các hình khối phổ biến trong diện tích hình vuông mà bạn thường xuyên bắt gặp trong các giáo trình toán học hiện đại:
| Loại hình khối | Thông số đầu vào chính | Phương thức tính diện tích | Đặc thù cấu trúc |
| Hình vuông | Cạnh biên (a) | Bình phương chiều dài cạnh (a x a) | Bốn cạnh và bốn góc đều bằng nhau |
| Hình chữ nhật | Chiều dài (l) và rộng (w) | Tích của hai kích thước khác biệt | Các cặp cạnh đối diện bằng nhau |
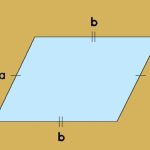
| Hình thoi | Hai đường chéo (d1, d2) | Nửa tích của hai đường chéo | Bốn cạnh bằng nhau nhưng góc thay đổi |
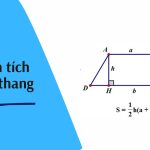
| Hình bình hành | Cạnh đáy (b) và chiều cao (h) | Tích của đáy với chiều cao tương ứng | Các cạnh đối song song và bằng nhau |
Việc nắm bắt sự khác biệt này cho thấy diện tích hình vuông luôn là bài toán có lời giải nhanh gọn nhất do giảm thiểu được số lượng biến số cần thu thập. Trong các ứng dụng kỹ thuật cao, sự đơn giản này giúp giảm thiểu khối lượng tính toán cho các hệ thống tự động hóa và phần mềm thiết kế chuyên dụng. Hơn nữa, tính cân bằng tuyệt đối của hình vuông còn mang lại vẻ đẹp thẩm mỹ trong kiến trúc, nơi mà diện tích bề mặt luôn được tối ưu hóa để tạo ra không gian sống hài hòa.
Kết luận
Diện tích hình vuông không chỉ dừng lại ở một công thức sách giáo khoa mà còn là chìa khóa giải mã nhiều vấn đề thực tiễn trong công việc và cuộc sống hàng ngày. Hy vọng rằng những phân tích chi tiết và các số liệu so sánh phía trên đã mang lại cho bạn một cái nhìn toàn diện và mới mẻ về chủ đề này. Đừng quên thường xuyên theo dõi các bài viết tiếp theo từ SevenAM để không bỏ lỡ những kiến thức giá trị và các xu hướng thời trang, đời sống đỉnh cao.