Số nguyên tố được ví như những viên gạch cơ bản nhất kiến tạo nên toàn bộ cấu trúc của hệ thống số tự nhiên rộng lớn mà nhân loại đang sử dụng hàng ngày. Những con số này chỉ sở hữu duy nhất hai ước số thực thụ, tạo nên một rào cản toán học vững chắc giúp bảo vệ dữ liệu trong kỷ nguyên số hóa hiện nay. Hãy cùng khám phá chiều sâu tri thức này thông qua góc nhìn mới mẻ và những phân tích chuyên sâu từ đội ngũ biên tập của SevenAM.
Những đặc tính nền tảng của số nguyên tố hiện nay
Việc nắm vững bản chất cốt lõi của các thực thể toán học này giúp chúng ta tiếp cận thế giới con số một cách có hệ thống và logic hơn. Đây là tiền đề quan trọng để giải quyết những bài toán phức tạp trong cả lý thuyết thuần túy lẫn các bài toán ứng dụng thực tiễn vào đời sống.
Khái niệm về các con số tự nhiên đặc thù
Xét về phương diện cấu trúc toán học, một đại lượng số tự nhiên được xếp vào nhóm đặc biệt này khi và chỉ khi nó sở hữu giá trị lớn hơn đơn vị và hoàn toàn không tồn tại khả năng bị chia cắt bởi bất kỳ số nguyên dương nào khác ngoại trừ chính thực thể đó và số một. Điều này tạo nên tính duy nhất và không thể phân rã của chúng trong mọi phép tính đại số phức tạp.
Quy tắc phân tách các hợp số cơ bản nhất
Mọi số tự nhiên lớn hơn một nếu không phải là số có tính chất đơn nhất thì đều có thể được biểu diễn dưới dạng một tích duy nhất của các thành phần cơ bản không thể chia nhỏ. Định lý cơ bản của số học khẳng định rằng sự phân rã này là duy nhất, ngoại trừ thứ tự của các thừa số, tạo nên tính ổn định tuyệt đối cho hệ thống toán học.
Cách nhận diện nhanh các số nguyên tố nhỏ
Trong phạm vi các số nhỏ, việc xác định tính chất này thường dựa vào các quy tắc chia hết cơ bản hoặc quan sát các chữ số tận cùng vốn thường là những số lẻ như một, ba, bảy hoặc chín. Tuy nhiên, ngoại lệ duy nhất và cũng là con số chẵn duy nhất trong dãy là số hai, điều này tạo nên một nét đặc trưng thú vị cho lĩnh vực nghiên cứu số học.
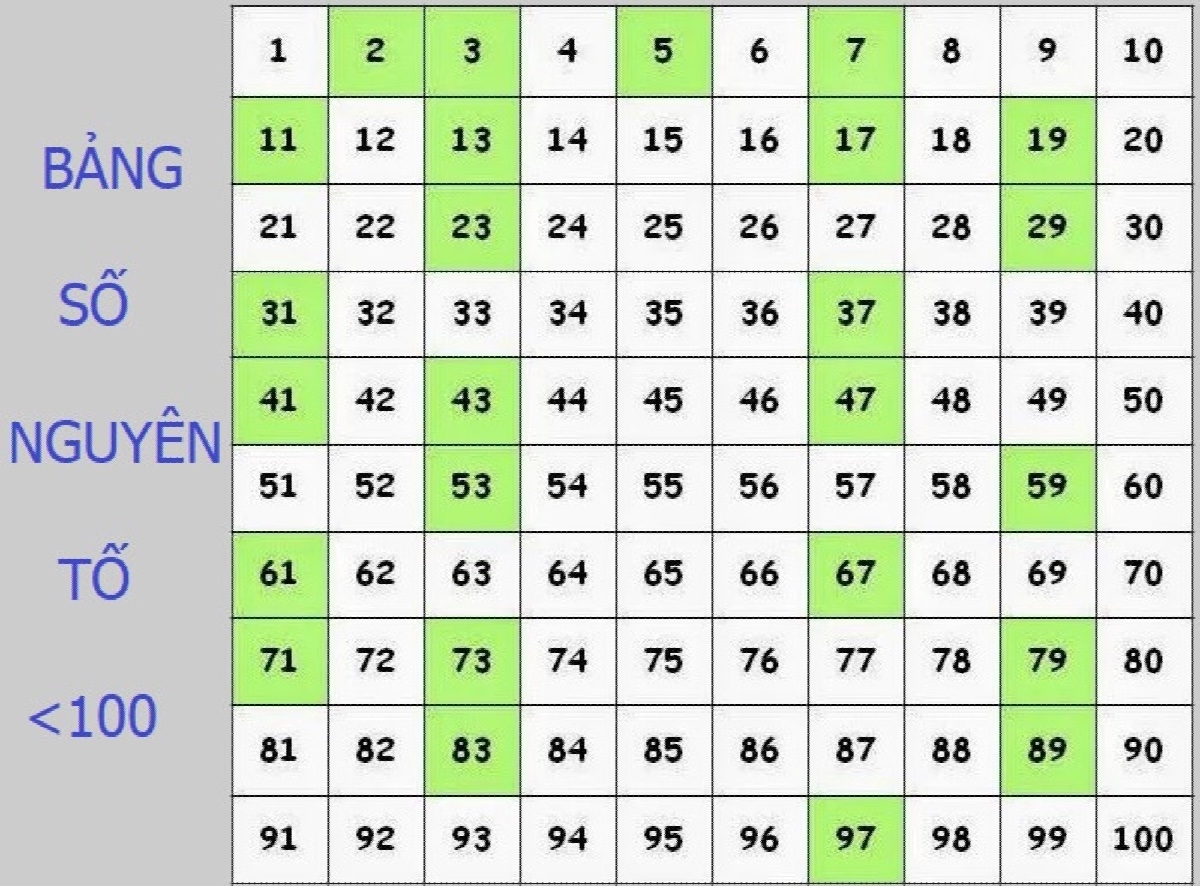
Các phương pháp tìm kiếm số nguyên tố hiệu quả nhất
Suốt hàng thiên niên kỷ qua, các nhà toán học đã không ngừng nỗ lực nghiên cứu và phát triển những thuật toán tối ưu nhất nhằm liệt kê dãy số nguyên tố này một cách chính xác. Dưới đây là những phương pháp phổ biến và mang tính lịch sử nhất mà cộng đồng toán học thế giới đang áp dụng:
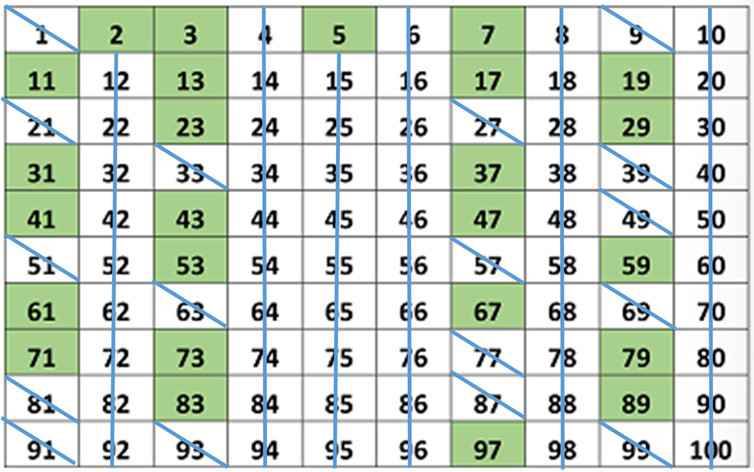
- Kỹ thuật sàng Eratosthenes cổ điển: Đây là một trong những phương pháp lâu đời nhất nhưng vẫn giữ nguyên giá trị bằng cách loại bỏ dần các bội số của các số đã biết để giữ lại những giá trị tinh khiết nhất trong một khoảng giới hạn cho trước.
- Kiểm tra tính nguyên tố dựa trên xác suất: Các thuật toán hiện đại như Miller-Rabin cho phép các nhà khoa học xác định khả năng một con số khổng lồ có phải là số nguyên tố hay không với độ chính xác gần như tuyệt đối trong thời gian ngắn.
- Công thức tìm kiếm Mersenne đặc biệt: Các nhà nghiên cứu tập trung khai thác các biểu thức toán học có dạng lũy thừa của hai trừ đi một để phát hiện ra những con số có quy mô hàng chục triệu chữ số.
- Ứng dụng định lý nhỏ của Fermat: Một công cụ lý thuyết vô cùng quan trọng giúp kiểm tra nhanh chóng các tính chất đặc thù của dãy số mà không cần thực hiện các phép chia tốn kém tài nguyên tính toán.
- Phân tích thừa số nguyên tố chuyên sâu: Quá trình này không chỉ giúp xác định tính chất của một số mà còn là chìa khóa để hiểu rõ cấu trúc liên kết giữa các con số trong hệ thống đại số hiện đại.
- Các dự án tính toán lưới toàn cầu: Sự kết hợp giữa hàng ngàn máy tính cá nhân trên khắp thế giới thông qua internet đã tạo ra một mạng lưới khổng lồ để săn tìm những kỷ lục mới về độ dài của các con số.
Vai trò của số nguyên tố trong công nghệ bảo mật
Trong thế giới kỹ thuật số đầy biến động, sự an toàn của các giao dịch trực tuyến và dữ liệu cá nhân phụ thuộc rất lớn vào độ phức tạp của các phép toán liên quan đến dãy số này. Các hệ thống mã hóa hiện đại hàng đầu đều lấy nền tảng từ sự khó khăn cực độ trong việc phân tích các số nguyên cực lớn thành các thành phần cơ bản.
Việc hiểu rõ cơ chế vận hành của các thuật toán mật mã giúp chúng ta nhận thấy tầm quan trọng không thể thay thế của toán học trong việc bảo vệ quyền riêng tư. Mỗi khi bạn thực hiện một giao dịch ngân hàng hoặc đăng nhập vào một ứng dụng, các thuật toán dựa trên số nguyên tố đang âm thầm hoạt động để ngăn chặn mọi nỗ lực xâm nhập trái phép.
Mã hóa RSA và sức mạnh bảo mật tuyệt đối
Hệ thống mật mã khóa công khai RSA hoạt động dựa trên nguyên lý là việc nhân hai số lớn rất dễ dàng nhưng quá trình ngược lại là tìm ra chúng từ một tích chung lại tốn hàng nghìn năm tính toán. Điều này tạo ra một “hầm trú ẩn” an toàn cho dữ liệu trước sức mạnh của các máy tính thông thường hiện nay.
Chứng chỉ SSL trong giao thức internet toàn cầu
Mọi trang web an toàn bắt đầu bằng giao thức HTTPS đều sử dụng các thuật toán dựa trên nền tảng của số nguyên tố để thiết lập kênh truyền tin được mã hóa giữa máy chủ và người dùng. Điều này đảm bảo rằng thông tin thẻ tín dụng hay mật khẩu của bạn không bị đánh cắp bởi các tin tặc trong quá trình truyền tải.
Bảo vệ thông tin tài chính cá nhân nhạy cảm
Các hệ thống ngân hàng hiện đại dựa vào tính chất khó phân rã của các số lớn để tạo ra các chữ ký số và mã xác thực giao dịch không thể làm giả. Sự bảo mật này là nền móng cho niềm tin của khách hàng vào hệ thống tài chính điện tử đang phát triển mạnh mẽ trên toàn thế giới.
Tương lai của mật mã học lượng tử hiện đại
Mặc dù máy tính lượng tử đang đe dọa các phương pháp truyền thống, nhưng các nhà khoa học vẫn đang nỗ lực tìm kiếm những dạng thức mới của các cấu trúc toán học này để đối phó với thách thức mới. Cuộc chạy đua giữa tấn công và phòng thủ trong không gian mạng sẽ luôn gắn liền với những khám phá mới về số học.
Thống kê và so sánh về các loại số nguyên tố
Trong quá trình nghiên cứu, các nhà toán học đã chia dãy số này thành nhiều nhóm khác nhau dựa trên những tính chất đặc thù và quy luật xuất hiện của chúng. Sự khác biệt giữa một số thông thường và một số mang tính chất đặc biệt như Mersenne hay số nguyên tố đôi thường nằm ở khoảng cách và công thức tạo ra chúng.
Dưới đây là bảng so sánh chi tiết giữa các nhóm số nguyên tố phổ biến để giúp bạn có cái nhìn tổng quan và sâu sắc hơn về sự đa dạng của chúng trong hệ thống toán học:
| Đặc điểm so sánh | Số nguyên tố thông thường | Số nguyên tố Mersenne |
| Công thức định nghĩa | Chỉ chia hết cho 1 và chính nó | Có dạng biểu thức
2n−12^n – 12n−1
|
| Tần suất xuất hiện | Xuất hiện thường xuyên ở các số nhỏ | Rất hiếm và khó tìm thấy |
| Ứng dụng chính | Giáo dục và lý thuyết số cơ bản | Kiểm tra hiệu năng siêu máy tính |
| Kỷ lục số chữ số | Thường được biết đến ở quy mô nhỏ | Lên tới hàng chục triệu chữ số |
| Cách thức tìm kiếm | Sàng Eratosthenes hoặc chia thử | Thuật toán Lucas-Lehmer chuyên biệt |
Sự phân bổ của các con số này trong dãy số tự nhiên không tuân theo một quy luật cố định nào nhưng lại có xu hướng thưa dần khi các giá trị tiến về vô hạn. Tuy nhiên, số lượng của chúng là vô tận, một sự thật đã được nhà toán học Euclid chứng minh từ hàng ngàn năm trước, thách thức mọi giới hạn tư duy của con người. Việc nghiên cứu các khoảng cách giữa hai số nguyên tố liên tiếp hiện vẫn là một trong những đề tài nóng hổi nhất, thu hút sự quan tâm của những bộ óc vĩ đại nhất trong làng toán học đương đại.
Kết luận
Số nguyên tố không đơn thuần là những khái niệm lý thuyết khô khan trong sách giáo khoa mà còn là chìa khóa then chốt mở ra cánh cửa của nền văn minh kỹ thuật số an toàn và bảo mật. Việc hiểu rõ và biết cách vận dụng những kiến thức này một cách thông minh sẽ giúp bạn tối ưu hóa tư duy logic cũng như nâng cao nhận thức về an toàn thông tin trong thời đại công nghệ 4.0. Đừng quên thường xuyên truy cập SevenAM để cập nhật thêm nhiều thông tin giá trị và làm giàu kho tàng tri thức của chính mình mỗi ngày.